
Angles Worksheets

To find the sum of the interior angles of a decagon, divide it up into triangles there are eight triangles because the sum of the angles of each triangle is 180 degrees we get. so, the sum of the interior angles of a decagon is 1440 degrees. More sum of the interior angles formula images. Formula to find the sum of sum of the interior angles formula interior angles of a n-sided polygon is. = (n 2) ⋅ 180°. by using the formula, sum of the interior angles of the above polygon is. = (6 2) ⋅ 180°. = 4 ⋅ 180°. = 720°---(1) by using the angles, sum of the interior angles of the above polygon is. = 120° + 90° + 110° + 130° + 160 + x°. No, a triangle can never have 2 right angles. a triangle has exactly 3 sides and the sum of interior angles sum up to 180°. so, if a triangle has two right angles, the third angle will have to be 0 degrees which means the third side will overlap with the other side. thus, it is not possible to have a triangle with 2 right angles.
Polygons Formula For Exterior Angles And Interior Angles Illustrated
Dec 12, 2016 · the sum of the interior angles, s, in an n-sided polygon can be determined using the formula s = 180(n 2), where n is the number of sides. benita solves this equation for n and writes the equivalent equation n = s/180 + 2. Therefore, the sum of the interior angles of the polygon is given by the formula: sum of the interior angles of a polygon = 180 (n-2) degrees interior angles of a polygon formula the interior angles of a polygon always lie inside the polygon. Jul 07, 2020 · the formula for finding the sum of the interior angles of a polygon is the same, whether the polygon is regular or irregular. so you would use the formula (n-2) x 180, where n is the number of sides in the polygon. A rhombus is a 4-sided polygon that has 4 equal sum of the interior angles formula sides. the diagonals of a rhombus bisects each other at right angles. area of rhombus = product of diagonals. area of rhombus (given length of side and an angle) area of rhombus = a 2 sin c where a is the length of the side and c is any interior angle.
Jul 07, 2020 · the formula for finding the sum of the interior angles of a polygon is the same, whether the polygon is regular or irregular. so you would use the formula (n-2) x 180, where n is the number of sides in the polygon. Linked here are exercises on angles formed by intersecting lines! know the congruent properties of vertical angles or vertically opposite angles and apply them to determine unknown angle measures. linear pairs of angles. two angles that are both adjacent and supplementary are a linear pair. the measure of such a pair sum up to 180°. See more videos for sum of the interior angles formula.
We can use a formula to find the sum of the interior angles of any polygon. in this formula, the letter n stands for the number of sides, or angles, that the polygon has. sum of angles = (n 2)180° let's use the formula to find the sum of the interior angles of a triangle. substitute 3 for n. In this video we explain the sum of the interior angles of a polygon. how to obtain the formula, and how to use it.
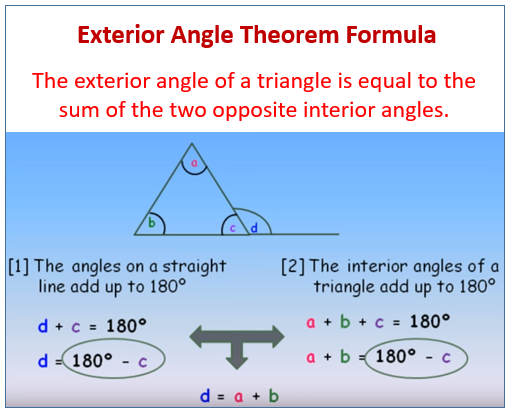
(n-2)x 180 degrees : the formula for finding the sum of all angles in a polygon ( regular). here "n" represents the number of sides of the polygon. for example . Angles on the inside of any triangle add up to 180. the length of one side of any triangle is always less than the sum and more than the difference of the lengths of the other two sides. an exterior angle of any triangle is equal to the sum of the two remote interior sum of the interior angles formula angles. other important triangles:.
Alternate interior angles. congruent angles inside parallel lines. find a formula for the sum of the angles in any polygon. parallelogram angles. An interior angle is an angle inside a shape. example: the interior angles of a triangle add up to 180°. let's try a sum of interior angles = (n−2) × 180°. Interior and exterior angle formulas: the sum of the measures of the interior angles of a polygon with n sides is (n 2)180. the measure of each interior angle of .
Geometry Lessons School Yourself
Sum of interior angles = (p 2) 180° sum of interior angles of a polygon formula: the formula for finding the sum of the interior angles of a polygon is devised by the basic ideology that the sum of the interior angles sum of the interior angles formula of a triangle is 1800. Formula for sum of exterior angles: the sum of the measures of the exterior angles of a polygon, one at each vertex, is 360°.
Sum of interior angles formula. the formula for the sum of that polygon's interior angles is refreshingly simple. let n n equal the number of sides of whatever regular polygon you are studying. here is the formula: sum of interior angles = (n − 2) × 180° s u m o f i n t e r i o r a n g l e s = ( n 2) × 180 °. Since a hexagon has 6 sides, let’s substitute that amount into the formula: sum of internal angles = (6 2) x 180 the sum of the interior angles would always be the same, but the value of. Set up the formula for finding the sum of the interior angles. the formula is s u m = ( n − 2 ) × 180 {\displaystyle sum=(n-2)\times 180} where s u m {\displaystyle sum} is the sum of the interior angles of the polygon, and n {\displaystyle n} equals sum of the interior angles formula the number of sides in the polygon. [1]. Sum of interior angles formula. this formula allows you to mathematically divide any polygon into its minimum number of triangles. since every triangle has .
0 Response to "Sum Of The Interior Angles Formula"
Posting Komentar